静态分析(Static Analysis) 是指在实际运行程序P之前,通过分析静态程序P本身来推测程序的行为,并判断程序是否满足某些特定的 性质(Property)。数据流分析作为静态分析的一种,可以解决程序分析中的一些问题,如存活变量分析。
静态分析
定义
静态分析(Static Analysis) 是指在实际运行程序P之前,通过分析静态程序P本身来推测程序的行为,并判断程序是否满足某些特定的 性质(Property)
性质(Property)
- 程序P是否会产生私有信息泄漏(Private Information Leak),或者说是否存在访问控制漏洞(Access Control Venerability);
- 程序P是否有空指针的解引用(Null Pointer Dereference)操作,更一般的,是否会发生不可修复的运行时错误(Runtime Error);
- 程序P中的类型转换(Type Cast)是否都是安全的;
- 程序P中是否存在可能无法满足的断言(Assersion Error);
- 程序P中是否存在死代码(Dead Code, 即控制流在任何情况下都无法到达的代码);
完美的静态分析
满足以下两个条件:
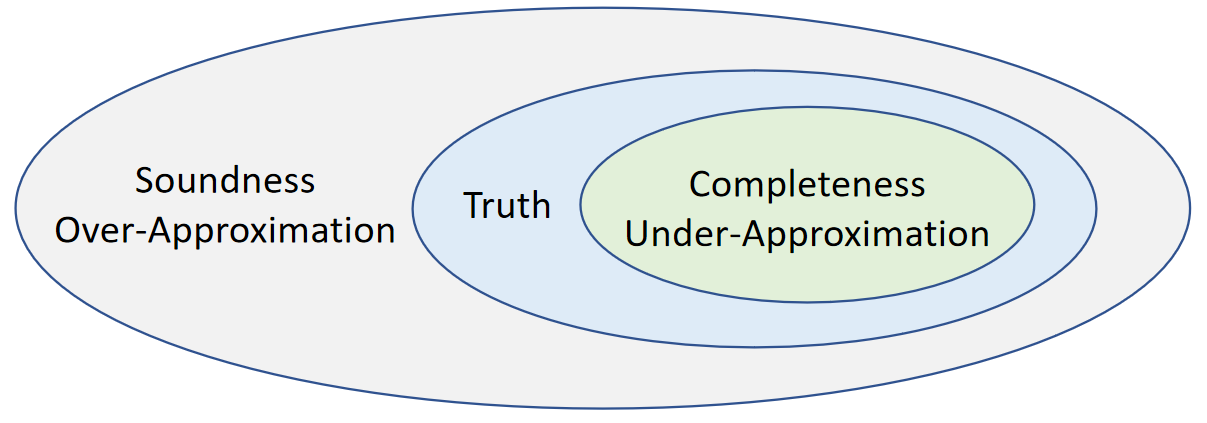
- 完整性(Soundness):真相一定在S给出的答案中;
- 正确性(Completeness):S给出的答案一定在真相中;
Rice定理(Rice Theorem)
对于使用 递归可枚举(Recursively Enumerable) 的语言描述的程序,其任何 有价值(Non-trivial) 的性质都是无法完美确定的。
- 关于递归可枚举,其含义是存在某个计算函数(可以是图灵机),能够将这种语言中的所有合法字符串枚举出来。这个概念有些抽象,不必深究,暂时只需要知道,目前我们所能想到的所有的编程语言都是递归可枚举语言。
- 关于有价值,我们认为,如果一种性质是所有的程序都满足的或者都不满足的,那么这种性质是没有价值的,除此之外的性质是有价值的。简单理解就是和程序运行时的行为相关的,让我们感兴趣的性质,就是有价值的性质。
妥协的静态分析
- 完整性(Soundness)=> 饱和估计(Overapproximate) => 分析结果存在False Positive => 这种分析称为Must Analysis
- 正确性(Completeness)=> 保守估计(Under-approximation)=> False Negative => May Analysis
数据流分析
数据流分析(Data Flow Analysis, DFA) 是指分析数据在程序中是怎样流动的。后文将详细介绍如下内容:
分析的对象:数据=基于抽象的特定数据
分析的基础:控制流图CFG
分析的行为:流动。不同的流动使用不同的处理方式。
- 在CFG的点(Node)内流动,即程序基块内部的数据流;=> 转移函数(Transfer Function)
- 在CFG的边(Edge)上流动,即由基块间控制流触发的数据流。=> 控制流处理方法(Control-Flow Handlings),通常称为汇集操作
分析的方式:安全估计(Safe-Approximation)
- 饱和估计(Over-Approximation)=> 可能性分析(May Analysis)
- 保守估计(Under-Approximation)=> 必然性分析(Must Analysis)
根据需求确定哪种是安全的。例如,编译优化通常使用必然性分析,如果优化了不应该优化的内容会导致程序错误。
数据流分析的主要内容
- 数据抽象(Data Abstraction)
- 流安全估计策略——饱和估计或者保守估计
- 转移函数(Transfer Function)、控制流处理方法(Control-Flow Handlings)
数据抽象
程序中的值有很多,但我们关心的只有和Non-trivial性质相关的值。比如考虑除0错误,只需要判断变量的值是否为0,其他的我们并不需要关心。
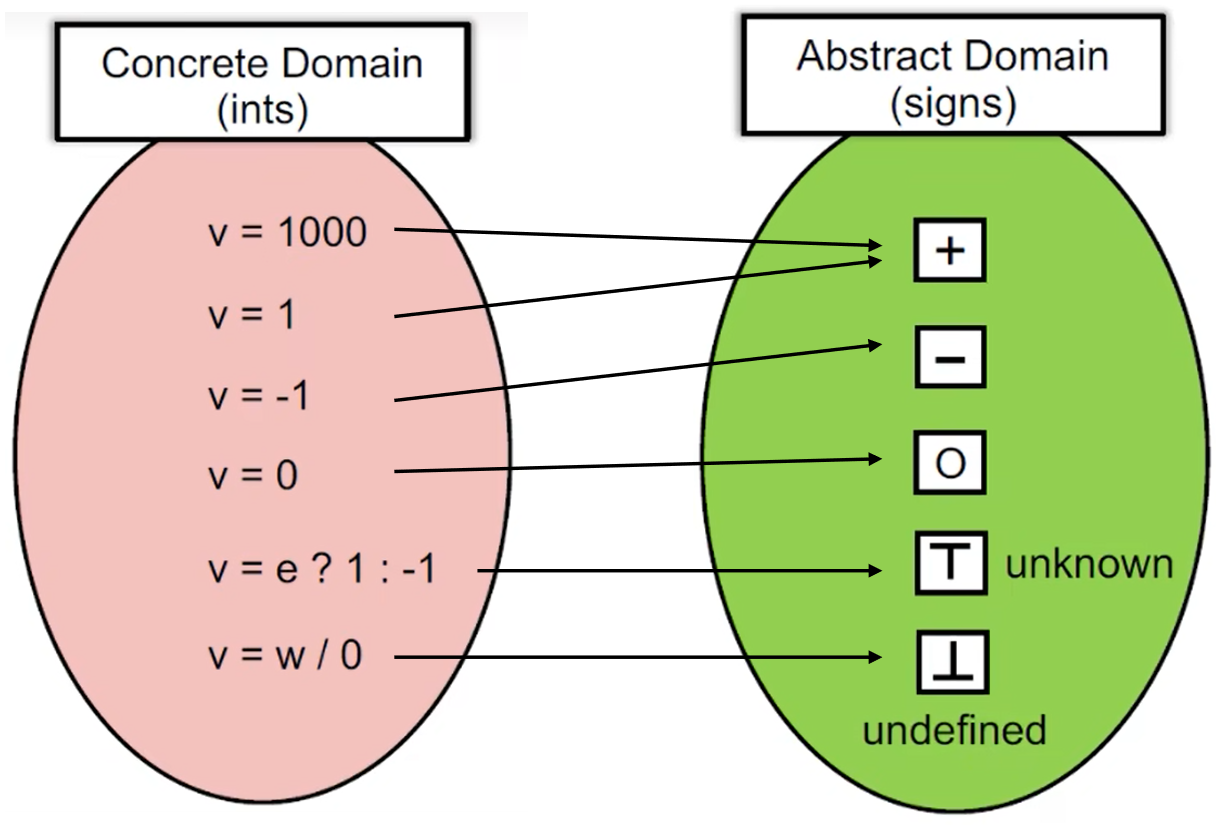
《举例:区分程序中所有变量的正负情况》
如下图,将变量值抽象成几类符号。然而,这样简单的抽象并不能解决全部的情况,对于未知的数据,我们定义为Unknown.
中间表示
中间表示通常作为静态分析的语言基础,便于进行分析,便于构建控制流图。
特点
- 低层次,和机器代码相接近
- 通常和具体的语言无关,主要和运行语言的机器(物理机或虚拟机)有关
- 简单通用
- 包含程序的控制流信息
控制流图
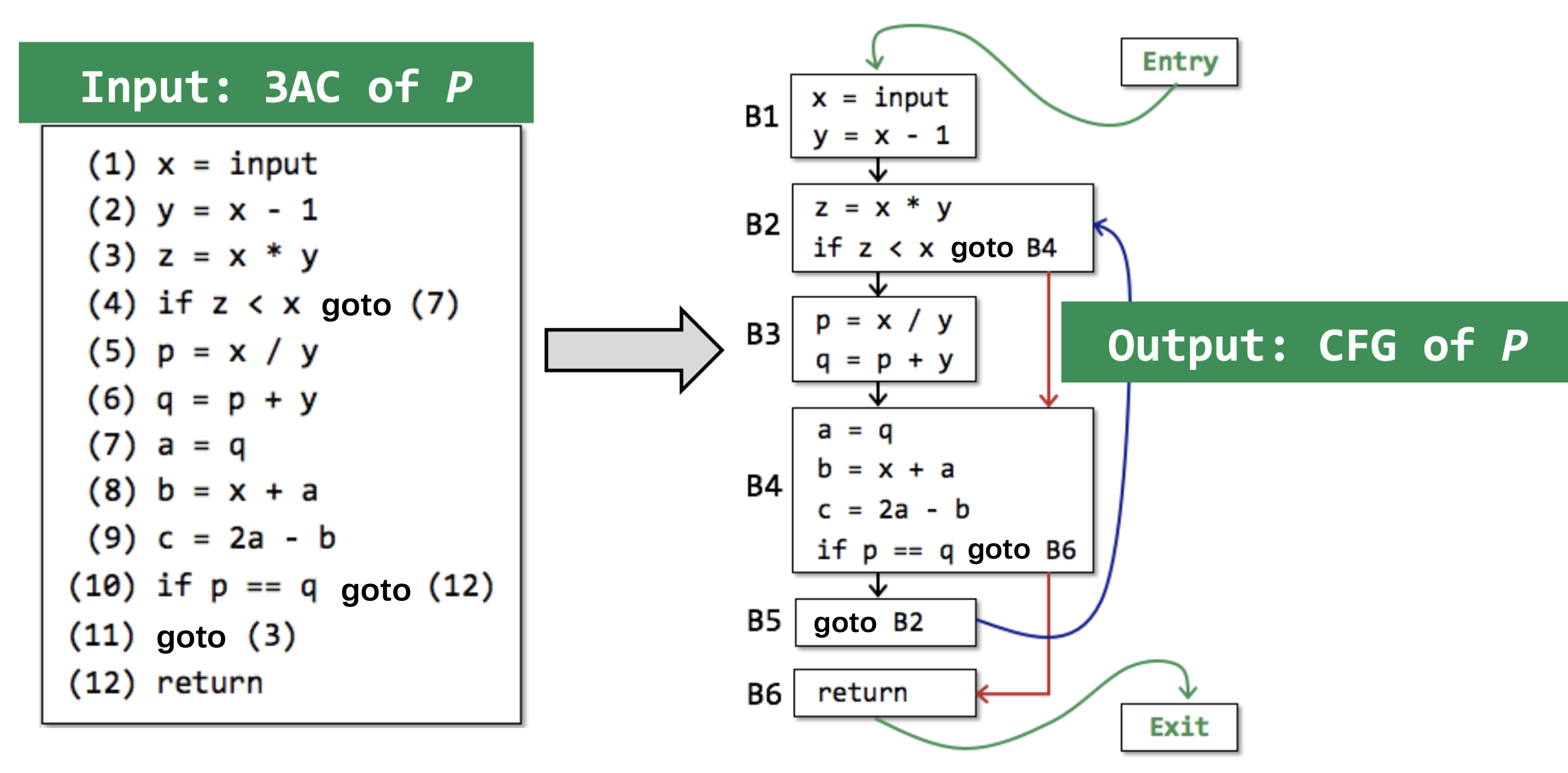
控制流图由Basic Block作为结点,以跳转语句作为边。
基块Basic Block
基块就是满足如下性质的最长指令序列:
- 程序的控制流只能从首指令进入
- 程序的控制流只能从尾指令流出
数据流分析 (过程内分析)
转移函数(Transfer Function)
转移函数定义了如何计算不同的语句的抽象数据的值。
在实际应用中,通常使用集合表示抽象数据,集合的内容表示了抽象数据的状态。在目标语句之前,程序的数据状态表示为In,在目标语句之后,程序的数据状态表示为Out。
对于语句S,转移函数 f 表示为
$$
Out[S] = f_S(In[S])
$$
《举例:区分程序中所有变量的正负情况》
如下图所示,为针对该问题设计的转移函数。对于加法运算,如果两个正数变量相加,被赋值的变量也是正数。根据抽象出的数据状态,我们可以枚举出加法运算的所有情况,从而构造出加法运算的转移函数,以此类推构造出除法。
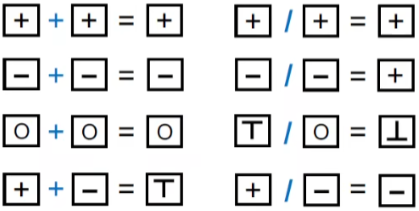
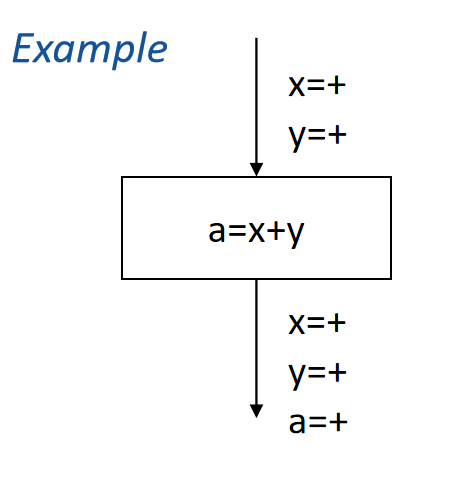
如下图所示为一个特定语句的分析样例。对于a=x+y语句,有In = ('x':'+','y':'+'),可以推断出a一定为正数,所以计算出Out = ('x':'+','y':'+','a':'+')
控制流处理方法(Control-Flow Handlings)
定义了如何计算控制流交汇的抽象数据的值。定义交汇时的运算为汇集 (meet,符号记作∧)。
对于一条语句而言,控制流的流向通常有以下几种情况:
- 输入为1条,输出为1条。这种情况为Basic Block内部的语句流向。
- 输入为1条,输出为2条。这种情况为分支语句,导致控制流分叉。
- 输入为多条,输出为1条。这种情况为跳转语句的指向语句,需要进行汇集操作。
汇集操作分为两类:
- 并集。通常会导致分析结果的饱和估计(Over-Approximation),最终导致May Analyze
- 交集。通常会导致分析结果的保守估计(Under-Approximation),最终导致Must Analyze
《举例:区分程序中所有变量的正负情况》
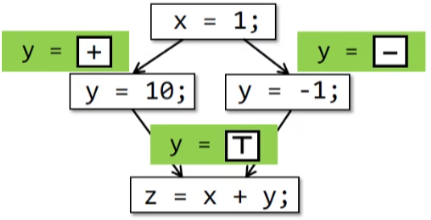
以下图的分析为例,对于分支导致y出现正负两种状态,在汇集时如果使用交集,则将y定义为Undefine(对应空)。如果使用并集,则将y定义为Unknown(对应全)
处理方法根据分析时采用的数据流向分为两类:
- 正向分析:符合正常的程序执行顺序,计算函数满足:
In[S] = ∧ Out[S_pre] - 反向分析:与正常的程序执行顺序相反,计算函数满足:
Out[S] = ∧ In[S_suc]
讨论
静态分析具有很多分析方法和实际应用,而数据流分析只是静态分析的一小部分。
静态分析还有很多其他的分析方式:控制流分析、污点分析、无效代码分析等等
还有很多应用场景:
- 编译器优化:死亡代码消除,代码移动
- 程序可靠性:空指针引用,内存泄露
- 程序安全性:隐私信息泄露,注入攻击
- 系统理解:IDE调用层次结构,类型指示
对于软件分析而言,静态分析也只是其中一类,并且因为静态带来的局限性,其存在很多无法解决的问题。另一种分析方式,动态分析,则通过执行程序的方式,获取动态信息,并以此提高分析的准确性。
同样,动态分析也有很多分析方式:指针分析、符号执行等等。
这里不在过多赘述,可以移步到 南京大学 李樾、谭添 老师在b站发布的软件分析课程视频. 也是本文作者的学习视频(文中用了很多视频中的图)
